A Bag Of Marbles Contains 3 Red Marbles 7 Blue Marbles And 5 Orange Marbles Calculate P Red

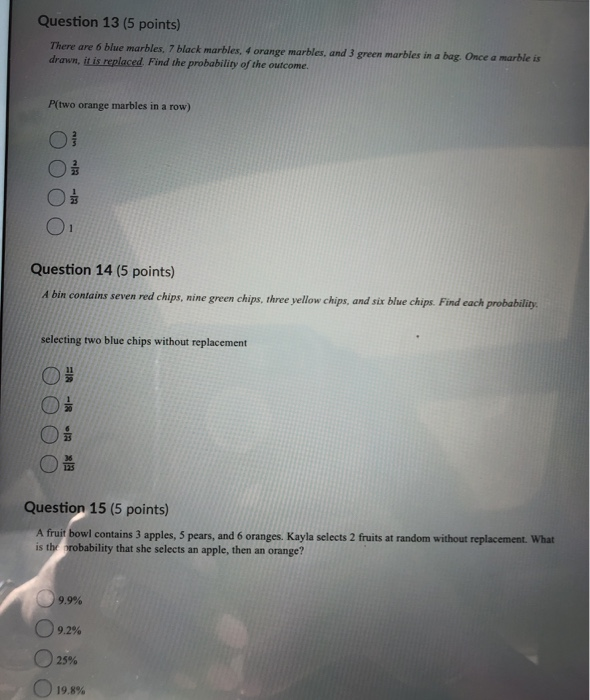
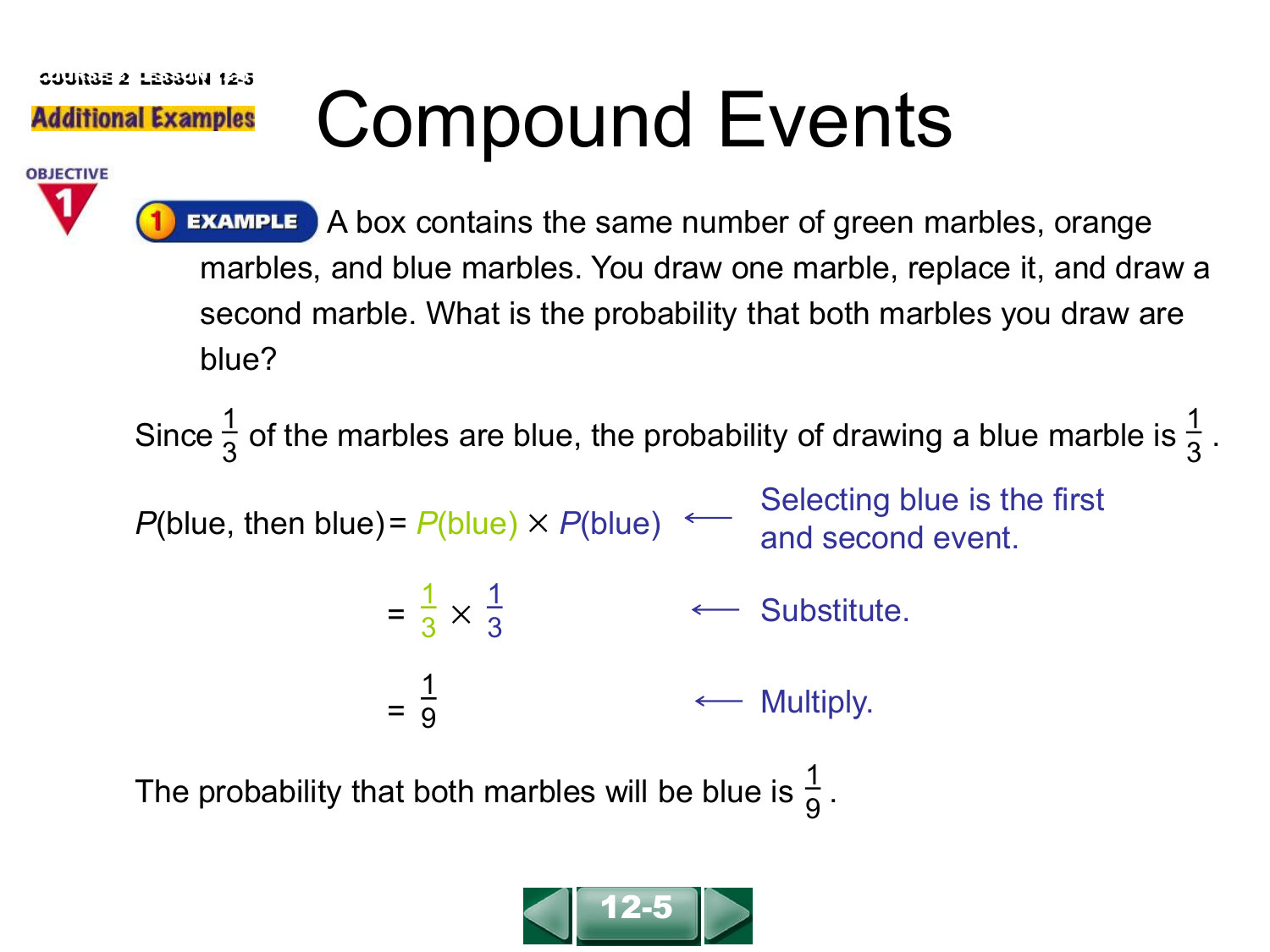
A marble is taken at random and replaced.

A bag of marbles contains 3 red marbles 7 blue marbles and 5 orange marbles calculate p red.

What is the probability of randomly selecting a blue marble then without replacing it randomly selecting a green marble. So they say the probability i ll just say p for probability. Work out the probability that the two marbles taken from the bag are the same color. You draw 5 marbles out at random without replacement.

A jar contains 4 black marbles and 3 red marbles. Probability of either happening p a p b 5 12 4 12 7 12 the key word in their question is red or green and that is why we add the two probabilities. Algebra linear inequalities and absolute value theoretical and experimental probability. The probability of picking a yellow marble.

Find the probability of pulling a yellow marble from a bag with 3 yellow 2 red 2 green and 1 blue i m assuming marbles. The problem asks for the probability of rr or bb. Two marbles are drawn without replacement. Total number of marbles in the bag is 3 4 7.

A draw the tree diagram for the experiment. Two marbles are drawn without replacement from a jar containing 4 black and 6 white marbles. B find probabilities for p bb p br p rb p ww p at least one red p exactly one red 3. What is the probability that exactly two of the marbles are red.

What is the probability that all the marbles are red. If they ask the probability of them both happening if they said red and green you would multiply p a p b. And so this is sometimes the event in question right over here is picking the yellow marble. Another marble is taken from the bag.